Graafisten tehtävien esimerkkejä ja ratkaisujen vaiheita LoggerProlla
- Pisteytyksen periaatteet
- Pisteytys Esimerkkinä YO 2 Syksy 2019
- LoggerPro hyötykäytössä
- Nopeus (x,t)-kuvaajasta / kaksi vaunua YO 4 Kevät 2019
- Interpolaatiolaskuri YO 2 Syksy 2019
Millä tavoin LoggerPron avulla voi kätevästi interpoloida ja ekstrapoloida - Laskettu sarake YO 9 Syksy 2019 (tavallista vaativampi esimerkki)
- Käyrän sovitus ja kysytyn suureen selvittäminen
Kurssin FY07 tehtävä (hajoamisvakio) - Nopeus (x,t)-kuvaajasta derivoimalla paikka ajan suhteen:
- YO 4 Kevät 2019 (mielenkiintoinen ratkaisu)
- YO 6 Kevät 2020 (tilanteen tarkastelu uudella tavalla)
- Nopeus (a,t)-kuvaajasta ja paikka (v,t)-kuvaajasta integroimalla
Tämä on yksi kätevä tapa käsitellä hyppyä voimalevyllä - Ylöspäin suuntautuvan hypyn tarkastelu imulssiperiaatteen avulla
HUOM! Tämä tulee myöhemmin
Yllä olevien YO- ja muiden tehtävien kysymykset ja aineistot ovat tehtävien yhteydessä.
YO Syksy 2019
LoggerPro
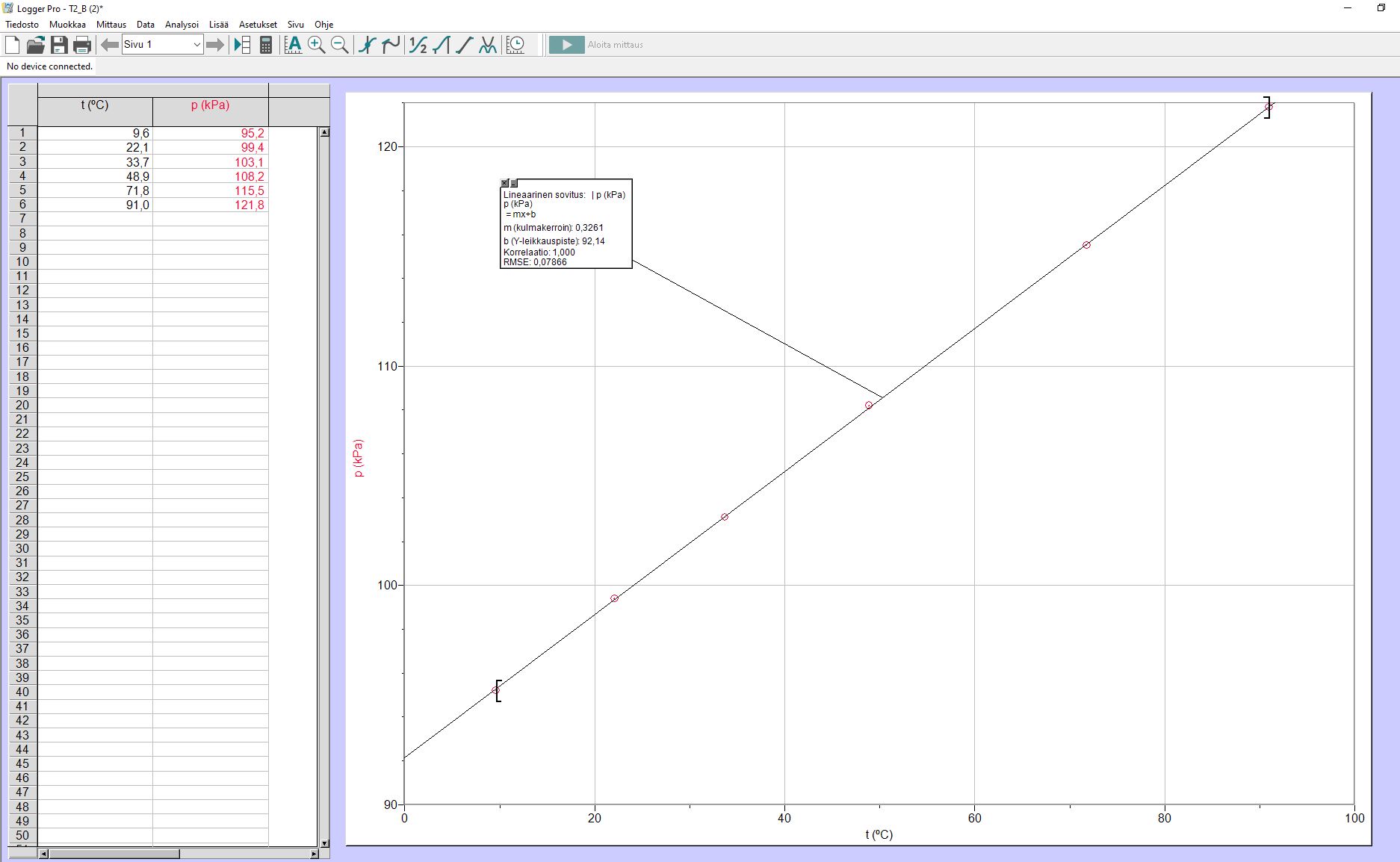
Pisteet 5 p:
- Akselit oikeinpäin
- Jakovälit järkevät
- Akseleilla suuretunnunkset ja yksiköt
- Mittapisteet näkyvissä
- Piirretty kuvaaja, lineaarinen riippuvuus
HUOM! Poista pisteiden yhdistäminen
HUOM! Tarkista, että käyrän yhtälö näkyy selvästi kuvakaappauksessa.
Interpolaatiolaskuri YO Syksy 2019
Tehtävä
Aineisto Tehtävä on yläpuolella
Tässä on todella kätevä käyttää LoggerPron Interpolaatiolaskuria. Tämä on eri asia kuin Analysointityökalun Interpoloi.
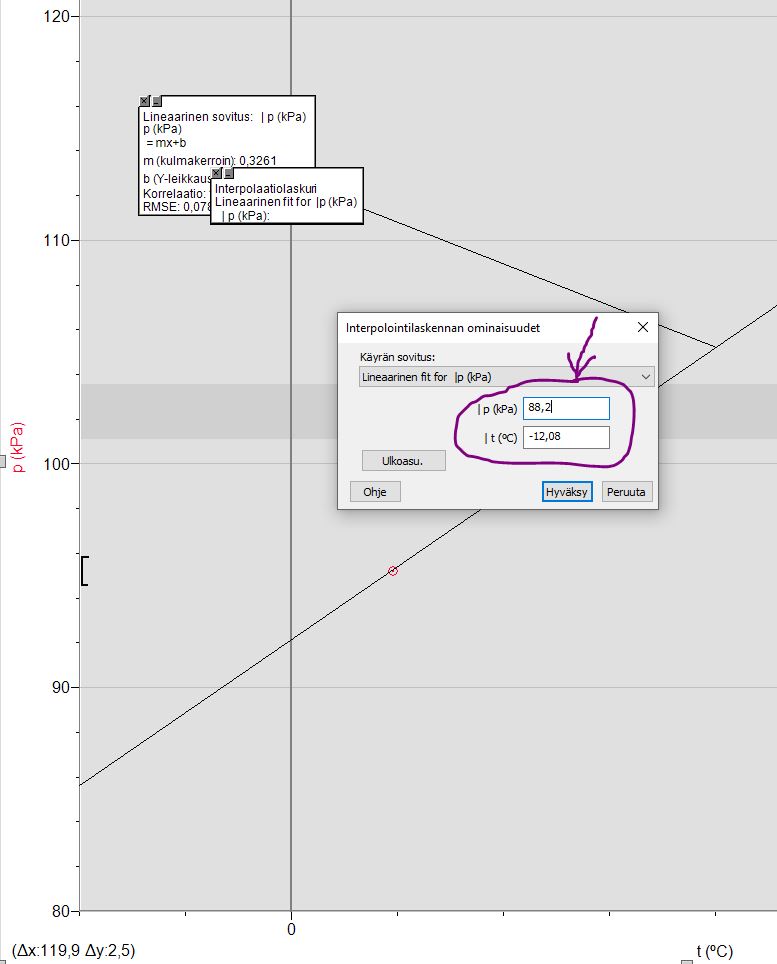
Interpolaatiolaskurin käyttö:
- Sovita käyrään sopiva yhtälö
- Laajenna tarvittaessa tutkittavaa aluetta
- Valitse Analysoi -> Interpolaatiolaskuri -> Aseta kysytty suureen arvo -> Kuvakaappaus
Tehtävä 9 Syksy 2019 / 20 p
Kohdassa 9.4 on kätevä käyttää LoggerPron Laskettua saraketta: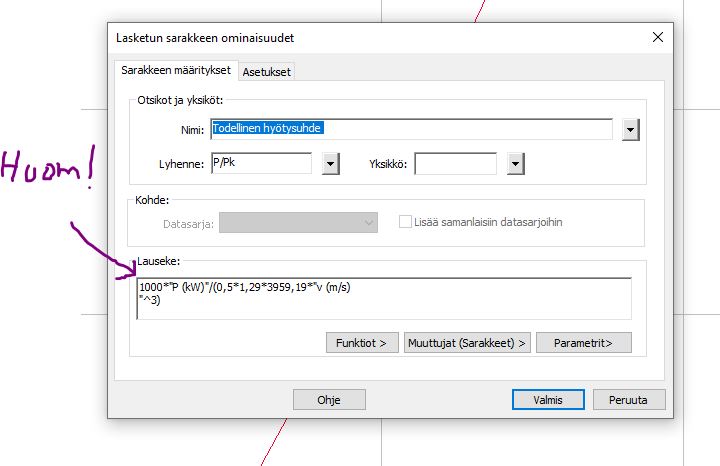 
Lasketun sarakkeen lausekkeessa tulee ottaa huomioon, että teho P on ilmoitettu yksikössä kW, minkä takia lauseke kerrotaan luvulla 1000:
Laskentaruudussa 1000*”P (kW)”/(0,5*1,29*3959,19*”v (m/s)”^3)
Tämä on poikkeuksellisen vaativa tehtävä, mutta laskettua saraketta on hyvä osata käyttää.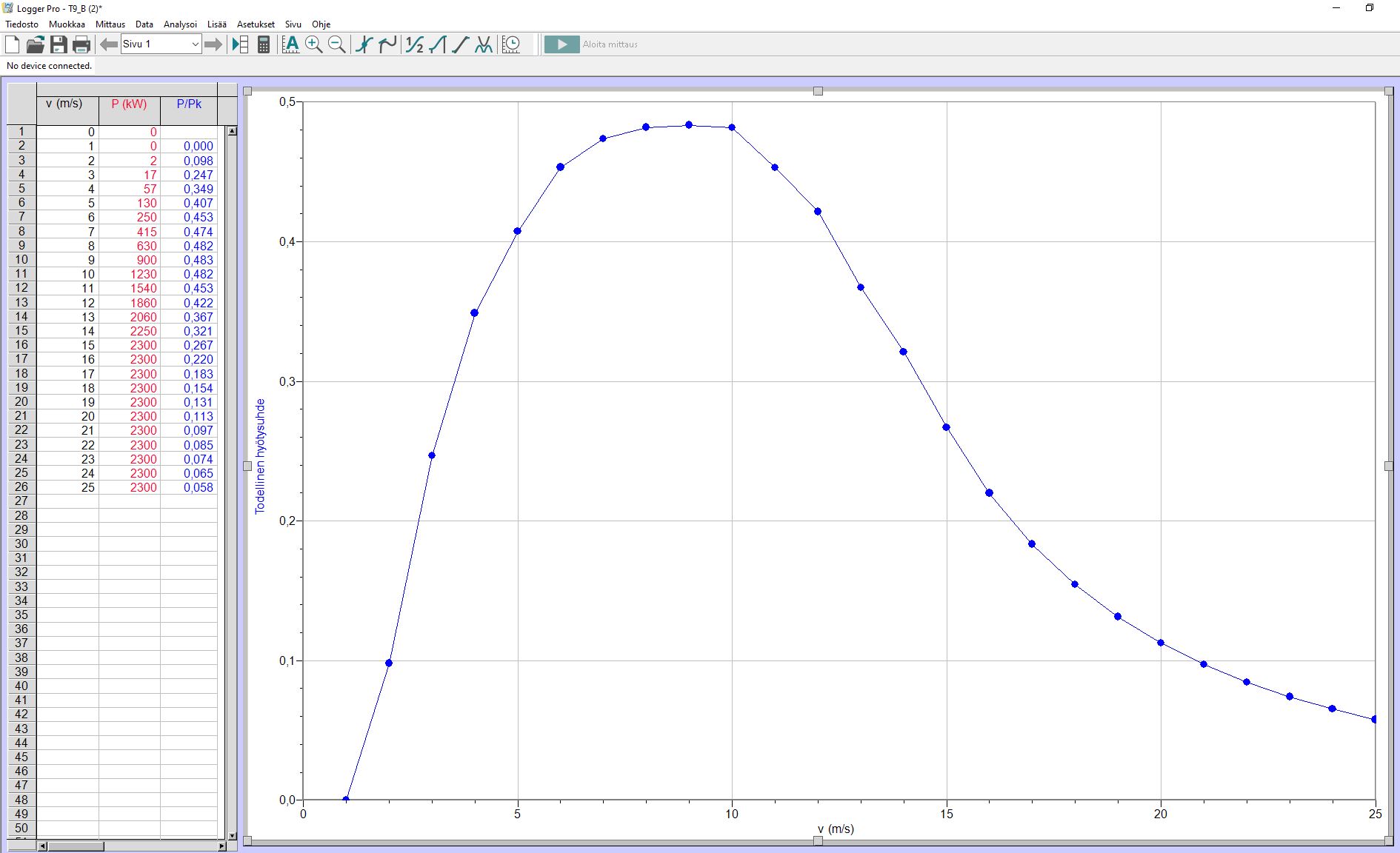 
YO Kevät 2020
LoggerPro
YO Kevät 2020 Tehtävä 7
LoggerPro
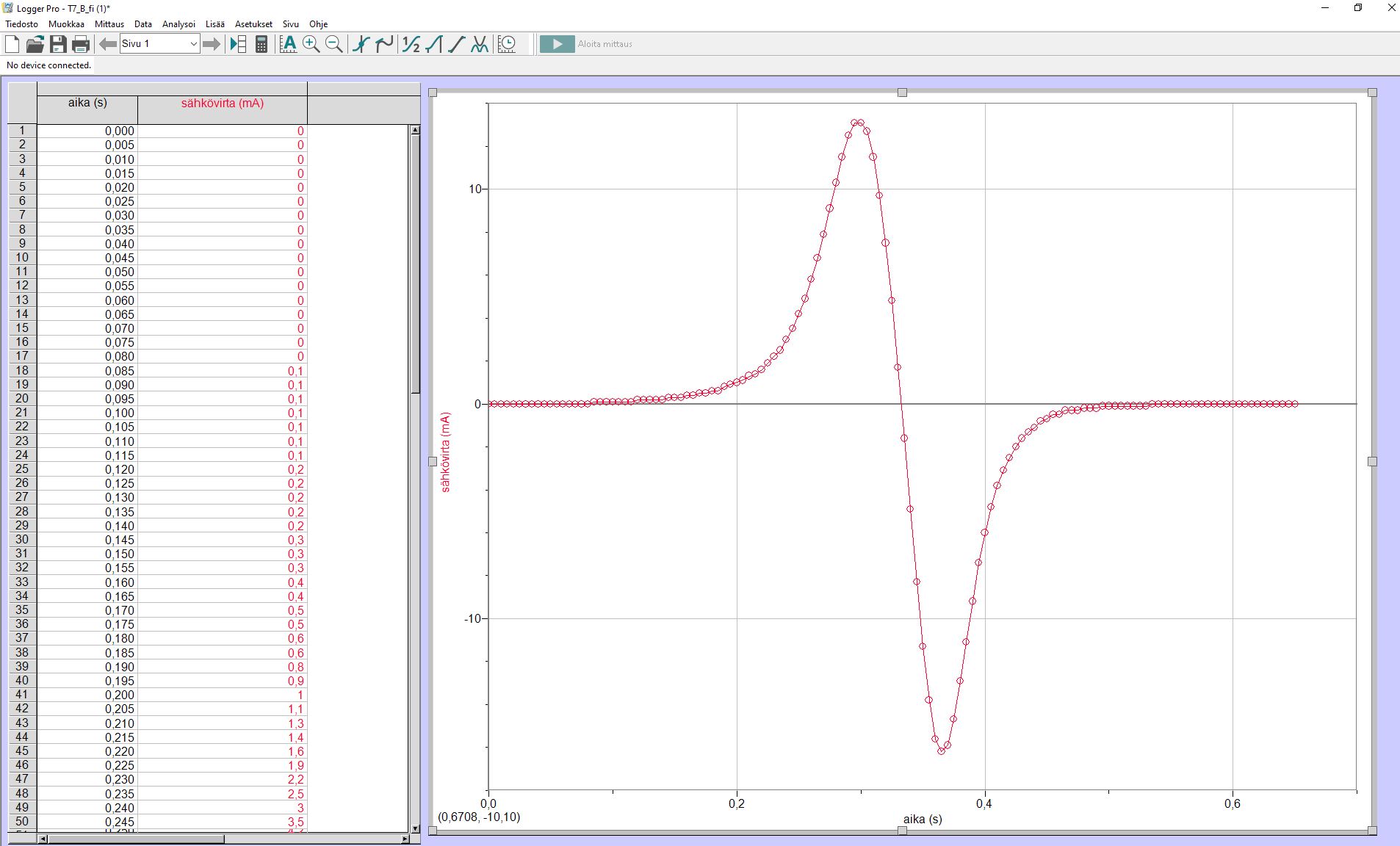
Pisteet
Fysiikan jaos tehtävät 6 ja 7:
Tässä kokeessa [kevät 2020] graafisia esityksiä arvioitiin kuitenkin hiukan aiempia vuosia sallivammin paristakin syystä: Mittauspisteitä oli kummassakin graafissa runsaasti, ja piirtämällä pisteitä yhdistävän viivan sai aikaan siistin kuvaajan, josta ei silmämääräisesti pystynyt päättelemään, esittikö graafi mitattuja pisteitä vai suureiden riippuvuuden kuvaajaa.
HUOM! Poikkeus:
Koska kummassakaan tehtävässä 6 ja 7 kuvaajan yksityiskohtainen muoto ei ollut oleellinen muiden tulosten laskemiselle, päätettiin hyväksyä myös sellaiset graafiset esitykset, joissa oli pelkkä pisteitä yhdistävä viiva tai pelkät havaintopisteet.
YTL:n linjaus: LINKKI
YO Syksy 2020
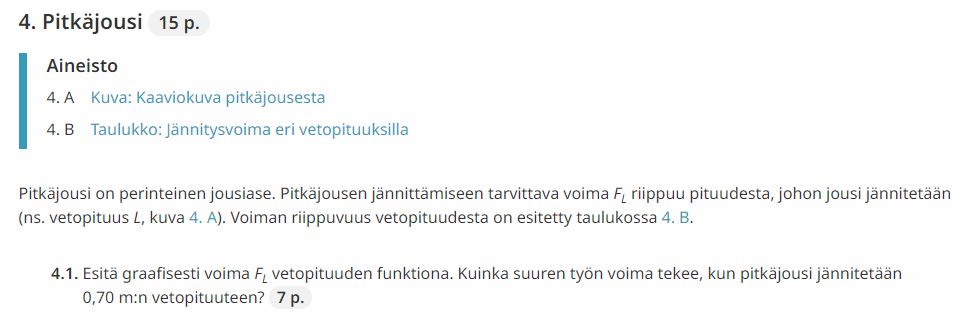
LoggerPro
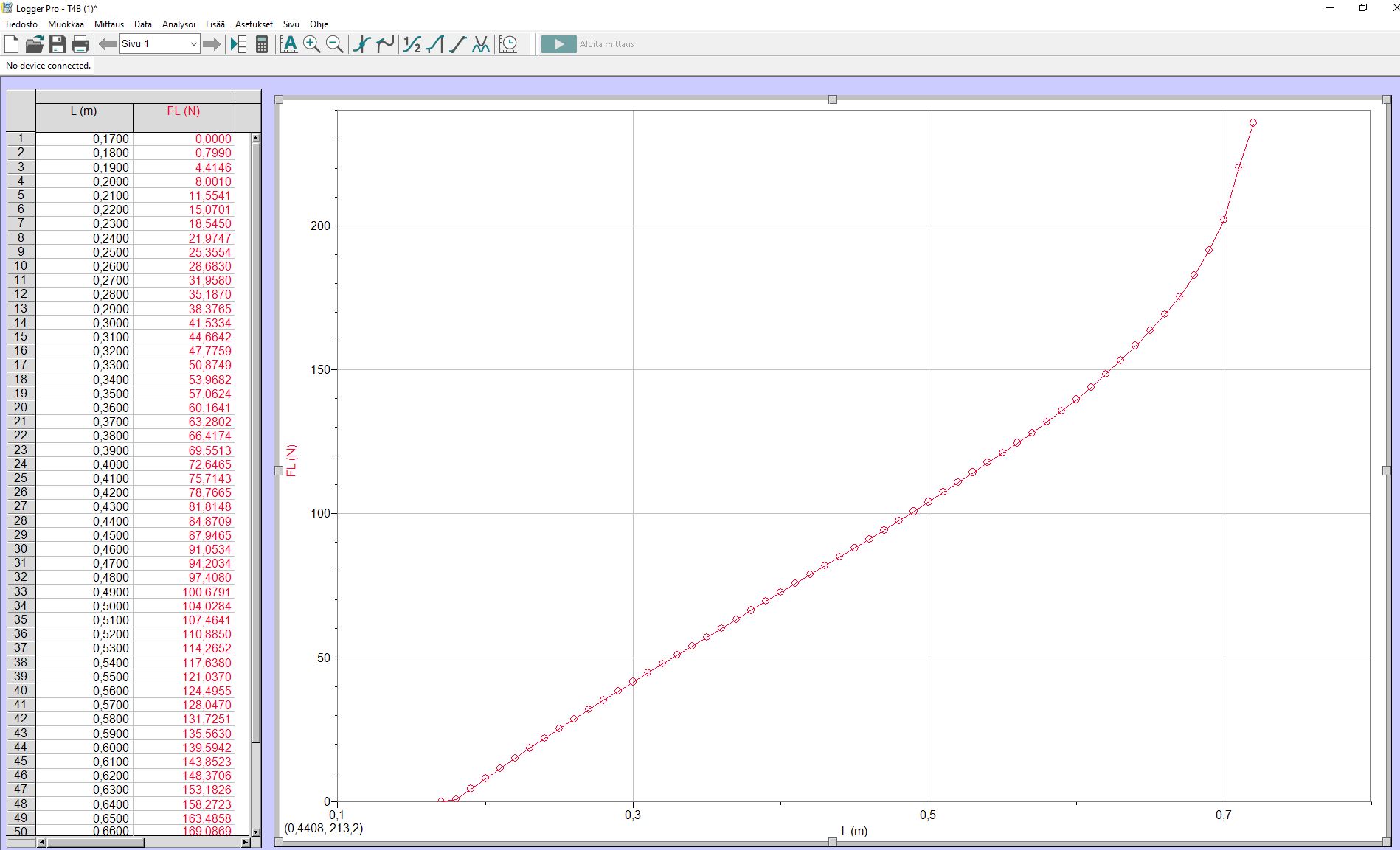
Pisteet
Kuvaajassa tulee olla pisteet TAI pisteet ja murtoviiva
Pelkkä murtoviiva olisi väärin…
OMA KOE
Kurssi FY07 / Hajoamisvakio & Puoliintumisaika
Tehtävä on alla
Aineisto
Annetun datan perusteella piirretään kuvaaja ja sovitetaan pistejoukkoon käyrä.
Muokataan hieman LoggerPron valmiita funktioita, koska aivan sopivaa ei ole tarjolla:
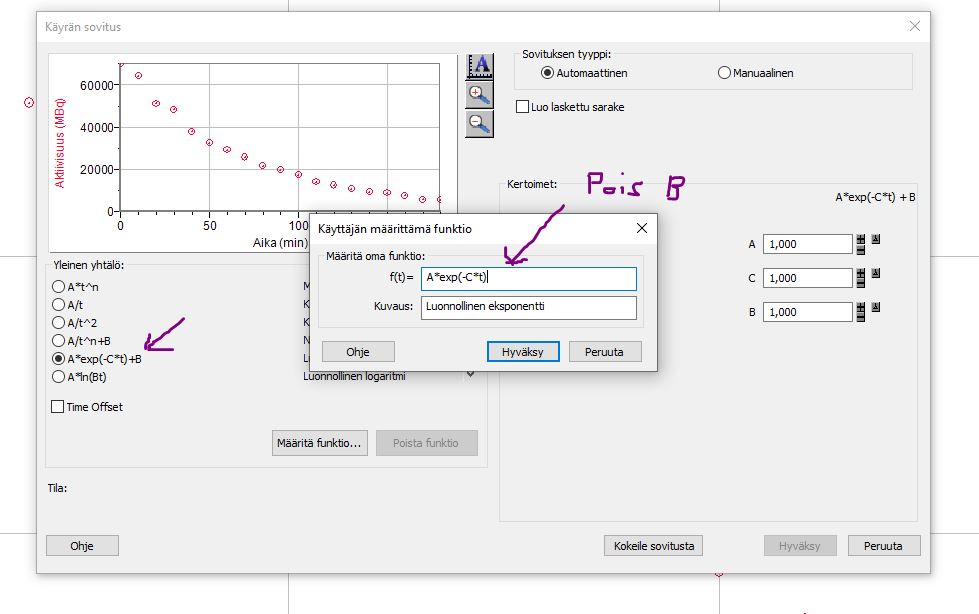
HUOM!
Varmistetaan, että käyrän yhtälö ja hajoamisvakio näkyy:
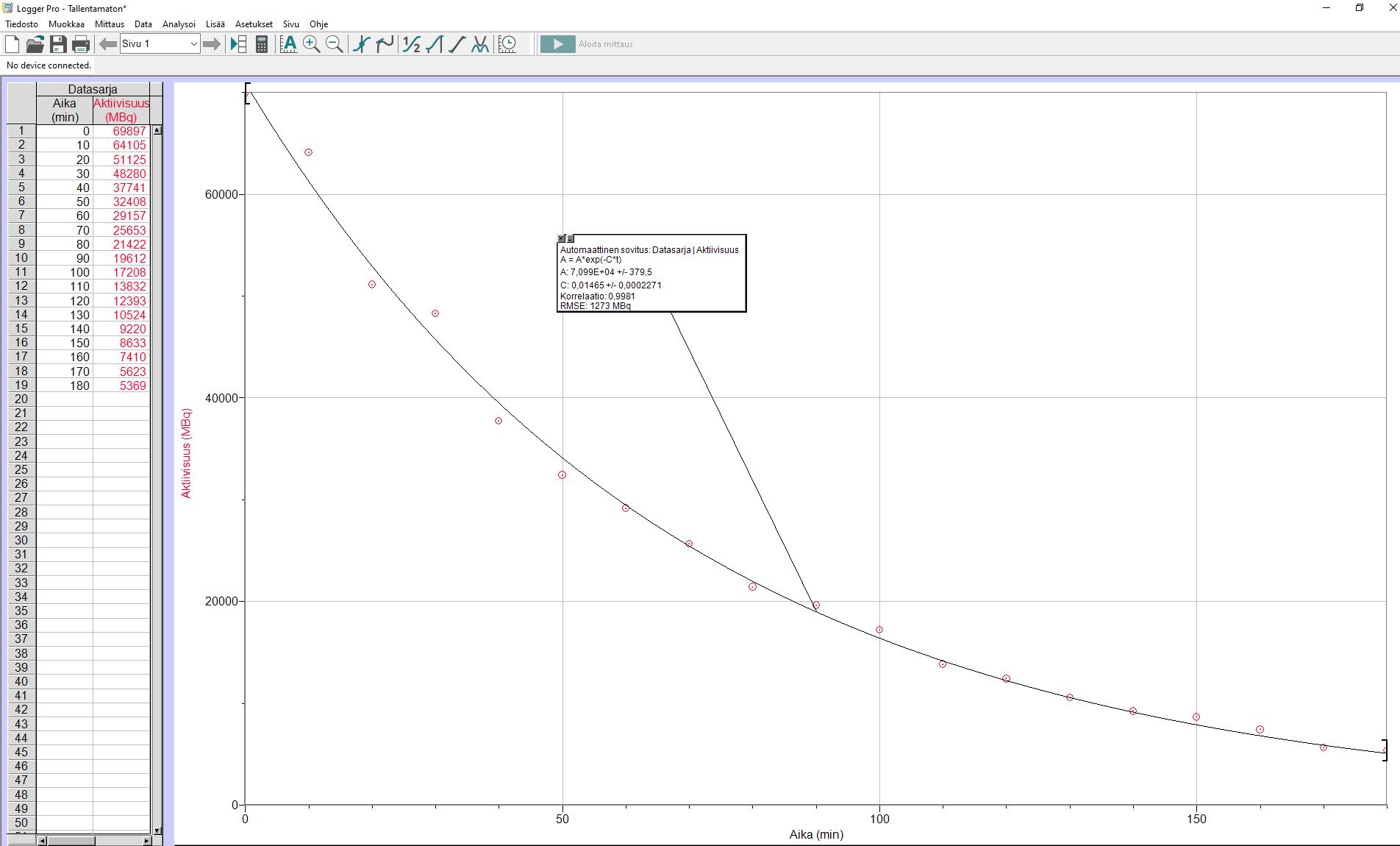
Hajoamisvakio on tässä C = 0,01465 1/s
YO Kevät 2019
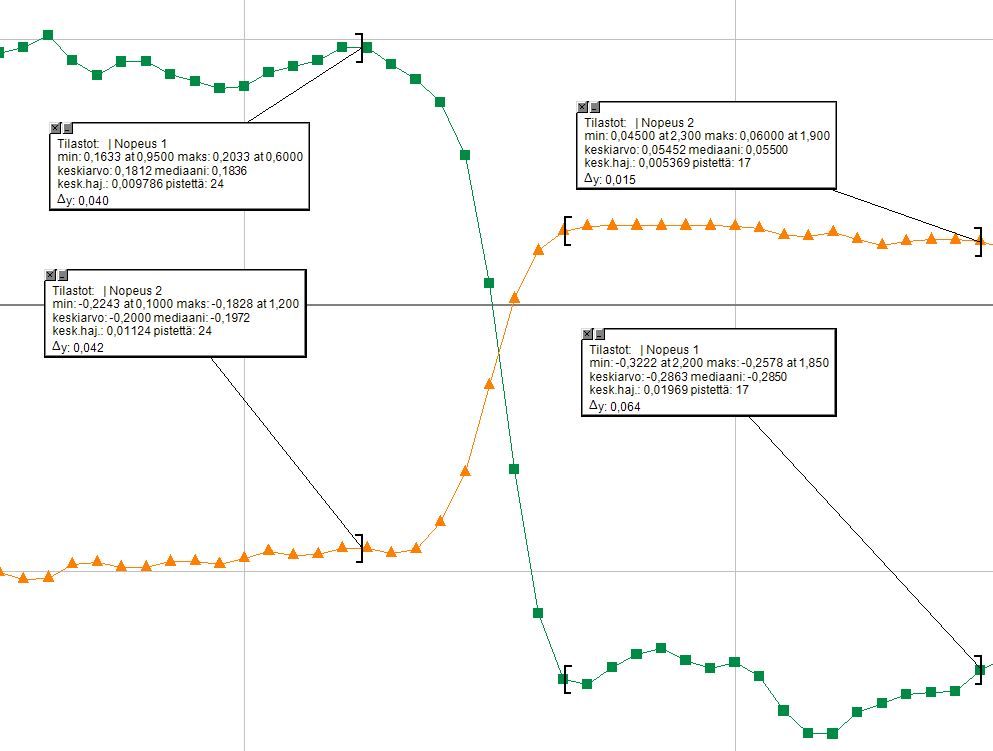
Saadaan piirrettyä paikka (x1 ja x2) ajan funktiona.
Suorien kulmakertoimet ovat kysyttyjä nopeuksia etumerkkeineen.
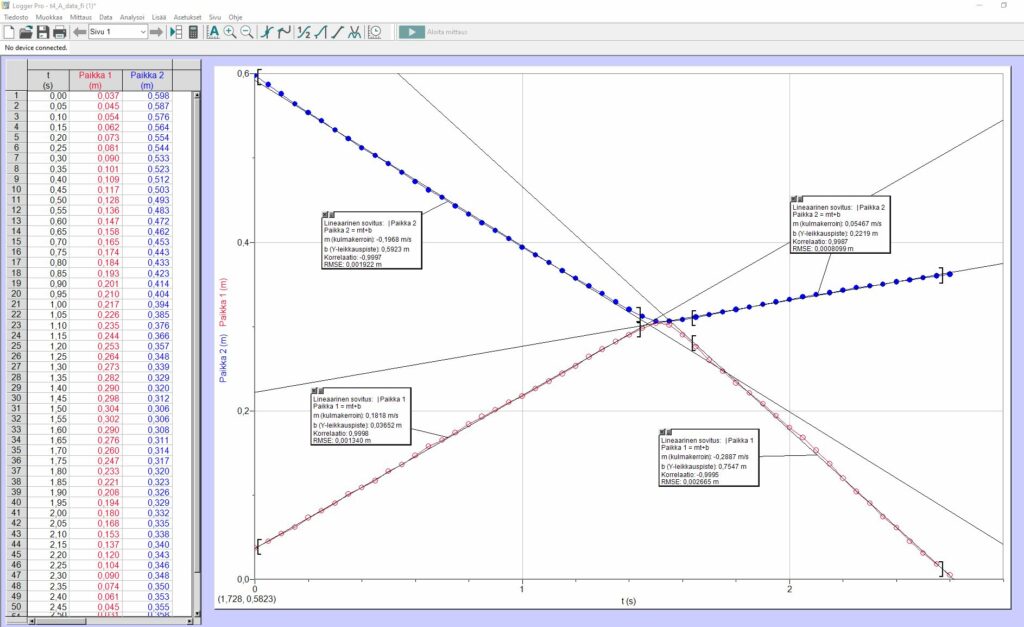
YO Kevät 2019 Tehtävä 4 (edellä)
Derivaatan käyttö
Tehtävän ratkaisussa on tärkeää osata muodostaa kaksi eri kuvaajaa ja neljä eri suoran yhtälöä.
Katso myös alla oleva ratkaisu, jossa on käytetty paikan derivaattaa ajan suhteen, jolloin saadaan nopeus v(t) = x´(t).
Derivaatan käyttö tulee perustella.
Derivaatta saadaan Funktioista, kun lasketaan uusi sarake.
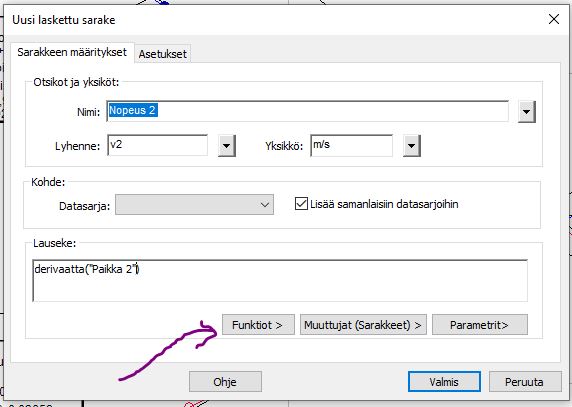
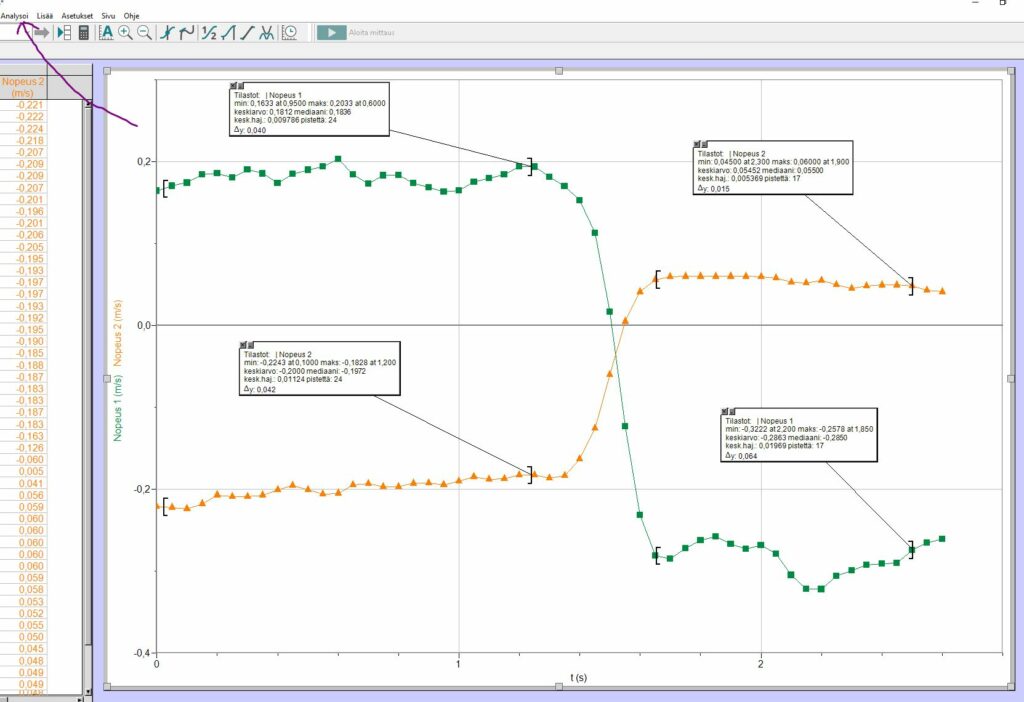
Nopeudet saadaan kätevästi:
Analysoi -> Tilastot -> Keskiarvo
YO Kevät 2020
Tehtävä 6
Derivointi
Tarkastellaan aineistoa ensin tavallisen kuvaajan (x,t) ja sitten derivaattafunktion (x´,t) eli (v,t) avulla
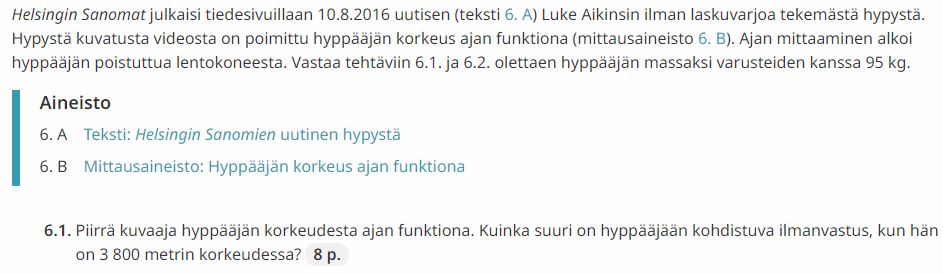
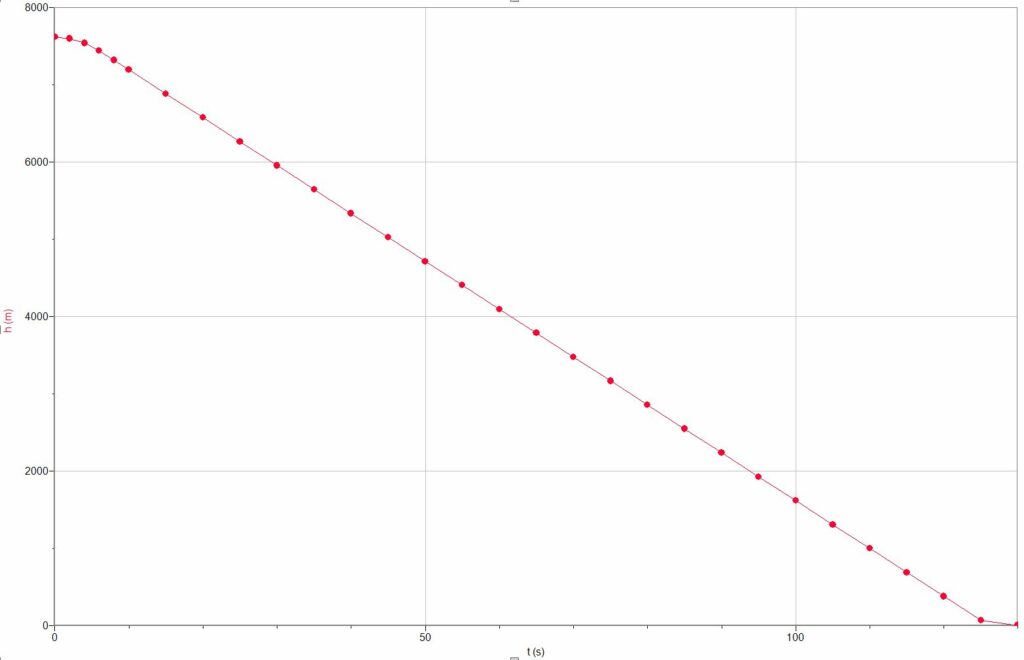
Käytetään LoggerPron derivaattafunktiota, jolloin saadaan nopeus paikan funktiona.
Katso ohjeet: Linkki
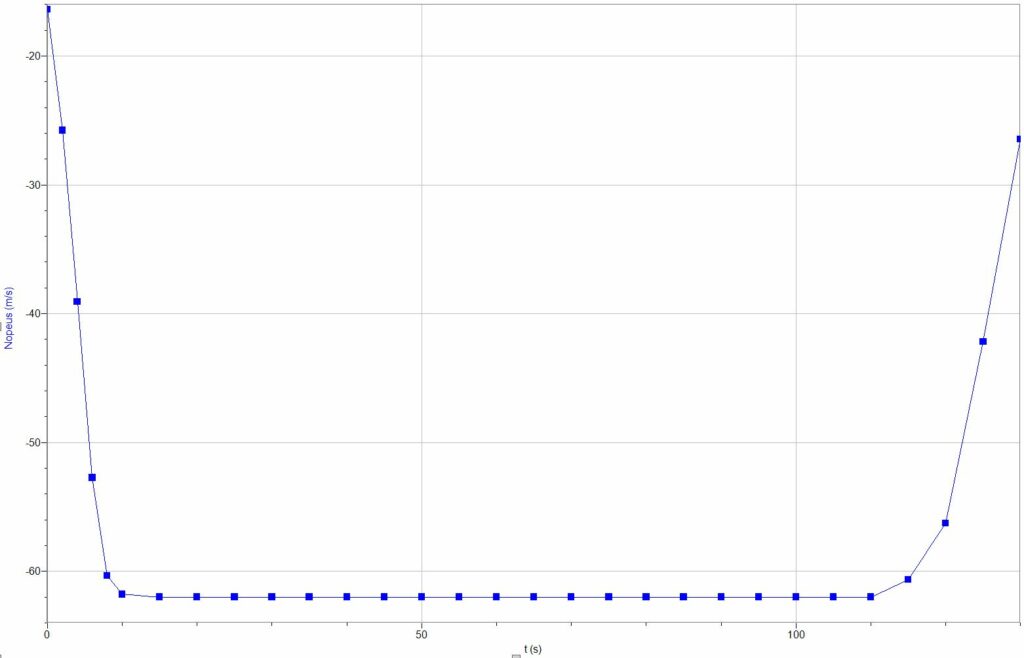
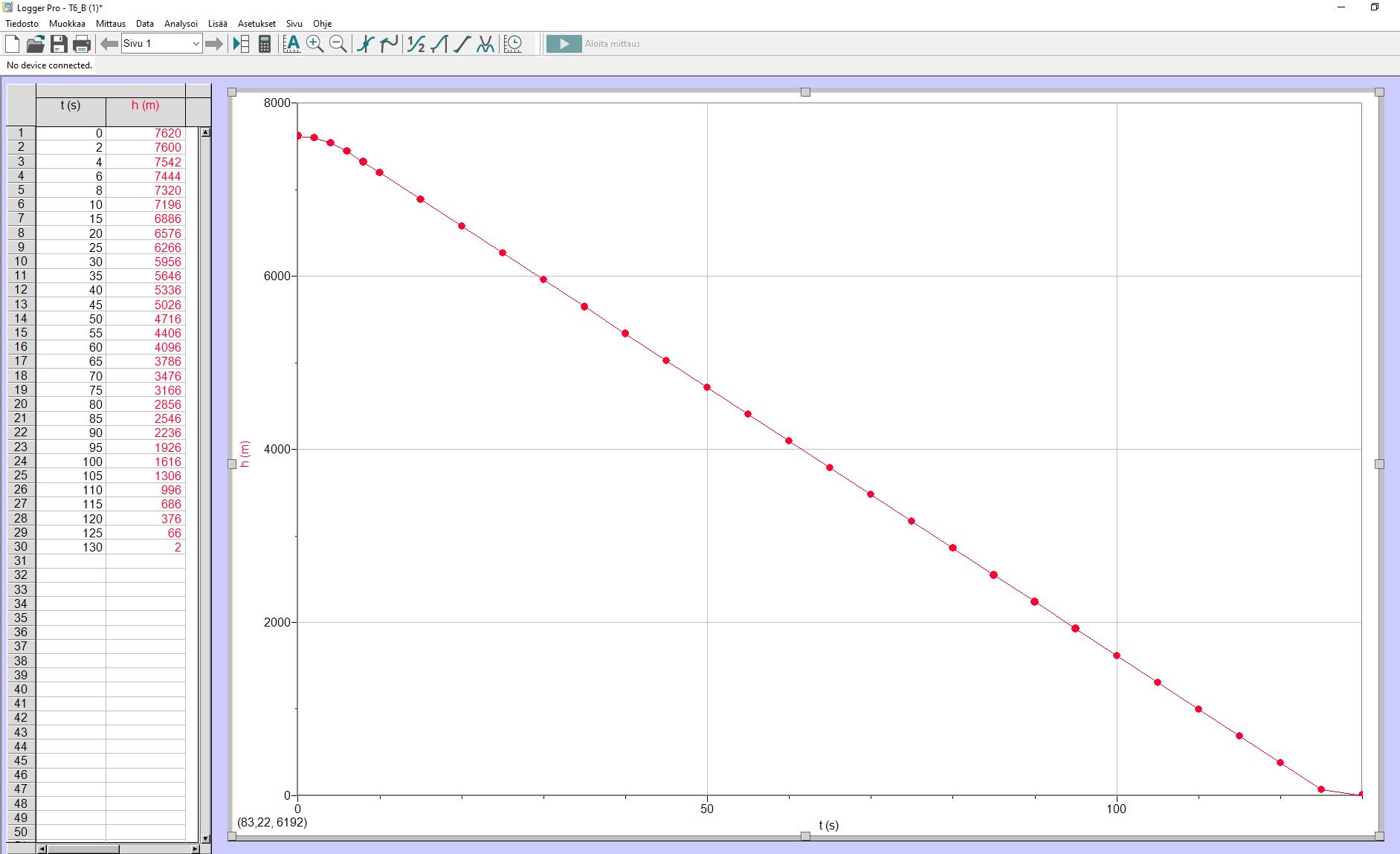
Hyppääjän nopeus on vakio, kun hän korkeudessa 3800 m.
Aikaa on kulunut tällöin lähdöstä 65 s.
Oma tehtävä: Voimalevy / ylöspäin suuntautuva hyppy
Tehtävä
Aineisto
Kiihtyvyys
Voimalevyn avulla saadaan mitattua henkilöön kohdistuva tukivoima ajan funktiona
Tukivoiman avulla saadaan helposti -> kokonaisvoima -> kiihtyvyys.
Nopeus
Käyttämällä LoggerPron integraalifunktiota saadaan kiihtyvyydestä a(t) nopeus v ajan funktiona.
Omia kokeiluja varten voit ladata mittausdatan omalle koneellesi:
Lataa tiedosto (LoggerPro)
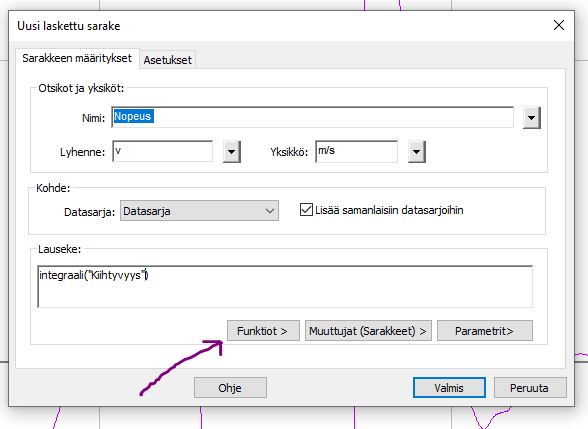
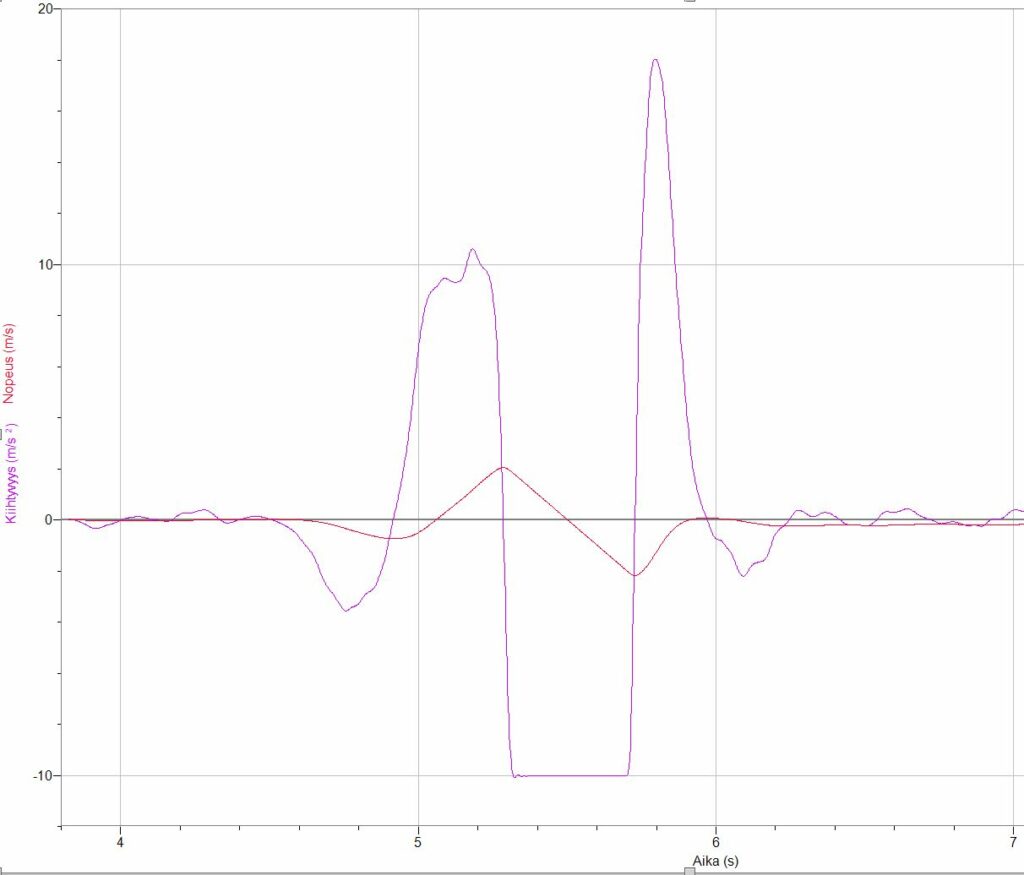
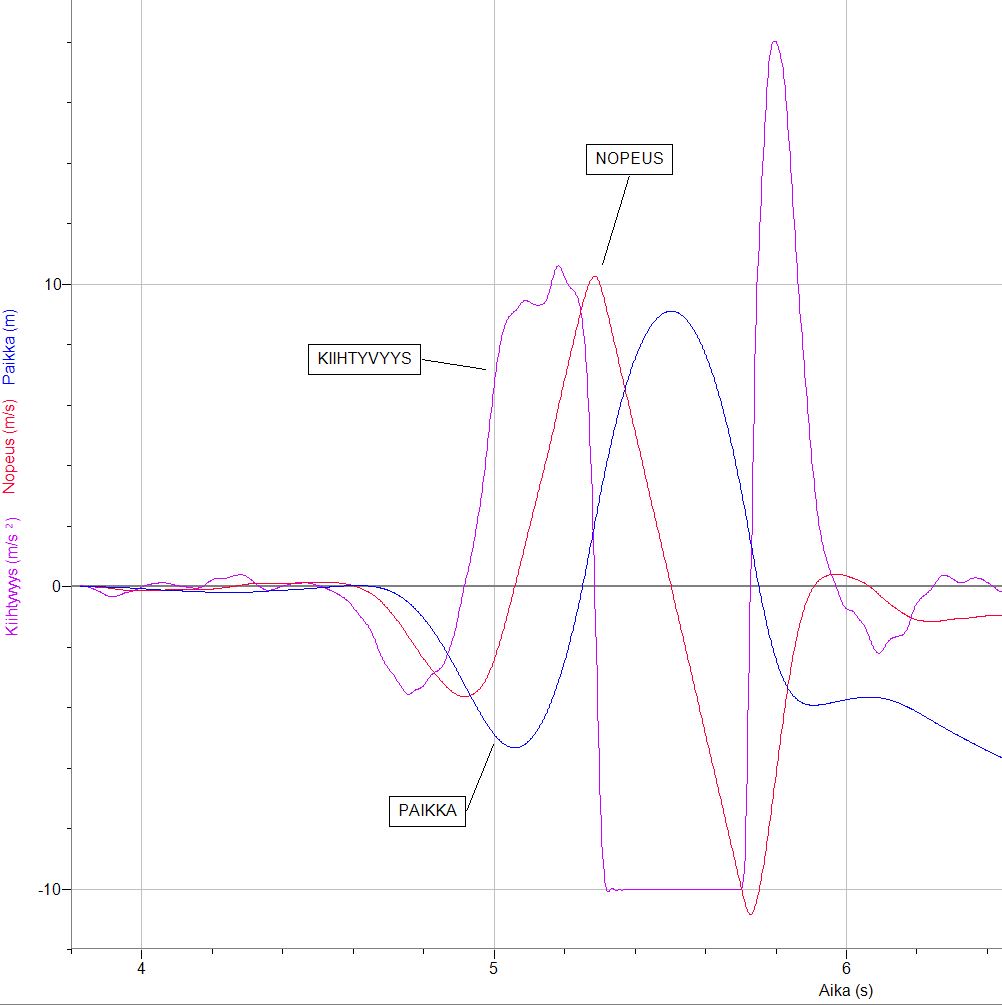
Yllä olevassa kuvassa suuremmat lukuarvot ovat kiihtyvyyden ja pienemmät nopeuden.
Paikka
Edelleen integroimalla nopeus v(t) saadaan paikka x ajan funktiona.
Paikan ja nopeuden arvot ovat pieniä verrattuna kiihtyvyyden lukuarvoihin.
Alla olevassa kuvassa on selvyyden vuoksi manipuloitu em. lukuarvoja.
